Creating a mesh sequence

In the previous demo, we saw how to create a TimePartition instance - one of the fundamental objects in Goalie. Another fundamental object is the mesh sequence, MeshSeq, which is built on top of a time partition. The idea is that a single mesh is associated with each subinterval.

For this and subsequent demos, we import from the namespaces of both Firedrake and Goalie.

from firedrake import *

from goalie import *

Again, turn debugging mode on to get verbose output.

set_log_level(DEBUG)

Consider the final subinterval from the previous demo.

end_time = 1.0
field_names = ["solution"]
dt = [0.125, 0.0625]
subintervals = [(0.0, 0.75), (0.75, 1.0)]
time_partition = TimePartition(
    end_time,
    len(subintervals),
    dt,
    field_names,
    num_timesteps_per_export=[2, 4],
    subintervals=subintervals,
)

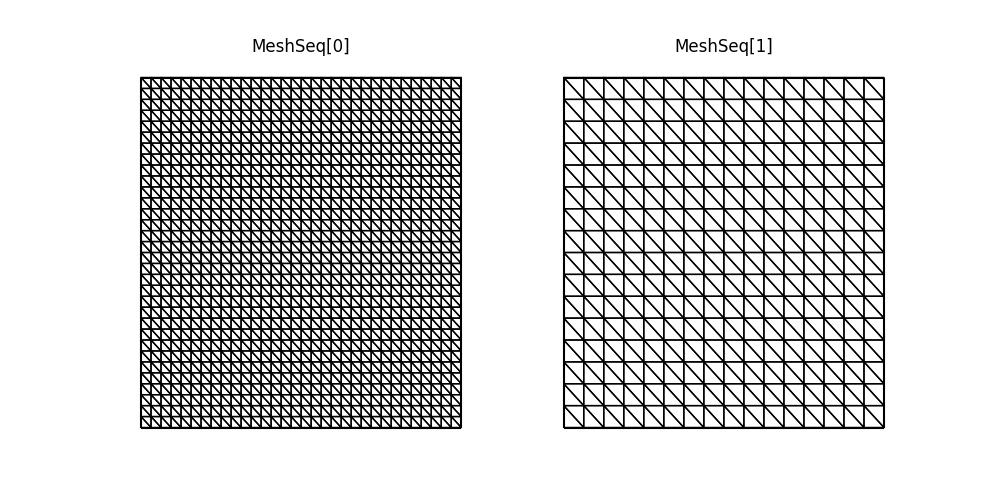
We use Firedrake’s utility UnitSquareMesh() function to create a list of two meshes with different resolutions.

m, n = 32, 16
meshes = [UnitSquareMesh(m, m), UnitSquareMesh(n, n)]

Creating a MeshSeq is as simple as

mesh_seq = MeshSeq(time_partition, meshes)

With debugging turned on, we get a report of the number of elements and vertices in each mesh in the sequence, as well as the corresponding maximal aspect ratio over all elements.

We can plot the meshes comprising the MeshSeq using the plot() method, provided they are two dimensional.

fig, axes = mesh_seq.plot()
fig.savefig("mesh_seq.jpg")

In the next demo, we solve an ordinary differential equation (ODE) using a special kind of MeshSeq.

This demo can also be accessed as a Python script.