Adjoint of Burgers equation¶
This demo solves the same problem as the previous one, but making use of dolfin-adjoint’s automatic differentiation functionality in order to automatically form and solve discrete adjoint problems.
We always begin by importing Goalie.
from firedrake import *
from goalie import *
For ease, the list of fields and functions for obtaining the solvers and initial
conditions are redefined as in the previous demo. The only difference is that now we
are solving the adjoint problem, which requires that the PDE solve is labelled with an
ad_block_tag that matches the corresponding prognostic variable name.
n = 32
mesh = UnitSquareMesh(n, n)
fields = [Field("u", family="Lagrange", degree=2, vector=True)]
def get_solver(mesh_seq):
def solver(index):
u, u_ = mesh_seq.field_functions["u"]
# Define constants
R = FunctionSpace(mesh_seq[index], "R", 0)
dt = Function(R).assign(mesh_seq.time_partition.timesteps[index])
nu = Function(R).assign(0.0001)
# Setup variational problem
v = TestFunction(u.function_space())
F = (
inner((u - u_) / dt, v) * dx
+ inner(dot(u, nabla_grad(u)), v) * dx
+ nu * inner(grad(u), grad(v)) * dx
)
# Time integrate from t_start to t_end
tp = mesh_seq.time_partition
t_start, t_end = tp.subintervals[index]
dt = tp.timesteps[index]
t = t_start
while t < t_end - 1.0e-05:
solve(F == 0, u, ad_block_tag="u") # Note the ad_block_tag
yield
u_.assign(u)
t += dt
return solver
def get_initial_condition(mesh_seq):
fs = mesh_seq.function_spaces["u"][0]
x, y = SpatialCoordinate(mesh_seq[0])
return {"u": Function(fs).interpolate(as_vector([sin(pi * x), 0]))}
In line with the firedrake-adjoint demo, we choose the QoI
which integrates the square of the solution \(\mathbf u(x,y,t)\) at the final time over the right hand boundary.
def get_qoi(mesh_seq, i):
def end_time_qoi():
u = mesh_seq.field_functions["u"][0]
return inner(u, u) * ds(2)
return end_time_qoi
Next, we define the TimePartition. In cases where we only solve over a
single time subinterval (as in this demo), the partition is trivial and we can use the
TimeInterval constructor, which requires fewer arguments.
end_time = 0.5
dt = 1 / n
time_partition = TimeInterval(end_time, dt, fields, num_timesteps_per_export=2)
Finally, we are able to construct an AdjointMeshSeq and
thereby call its solve_adjoint() method. This computes the QoI
value and returns a dictionary of solutions for the forward and adjoint
problems.
mesh_seq = AdjointMeshSeq(
time_partition,
mesh,
get_initial_condition=get_initial_condition,
get_solver=get_solver,
get_qoi=get_qoi,
qoi_type="end_time",
)
solutions = mesh_seq.solve_adjoint()
The solution dictionary is similar to solve_forward(),
except there are keys "adjoint" and "adjoint_next", in addition
to "forward", "forward_old". For a given subinterval i and
timestep index j, solutions["adjoint"]["u"][i][j] contains
the adjoint solution associated with field "u" at that timestep,
whilst solutions["adjoint_next"]["u"][i][j] contains the adjoint
solution from the next timestep (with the arrow of time going forwards,
as usual). Adjoint equations are solved backwards in time, so this is
effectively the “lagged” adjoint solution, in the same way that
"forward_old" corresponds to the “lagged” forward solution.
Finally, we plot the adjoint solution at each exported timestep by
looping over solutions['adjoint']. This can also be achieved using
the plotting driver function plot_snapshots.
fig, axes, tcs = plot_snapshots(
solutions, time_partition, "u", "adjoint", levels=np.linspace(0, 0.8, 9)
)
fig.savefig("burgers1-end_time.jpg")
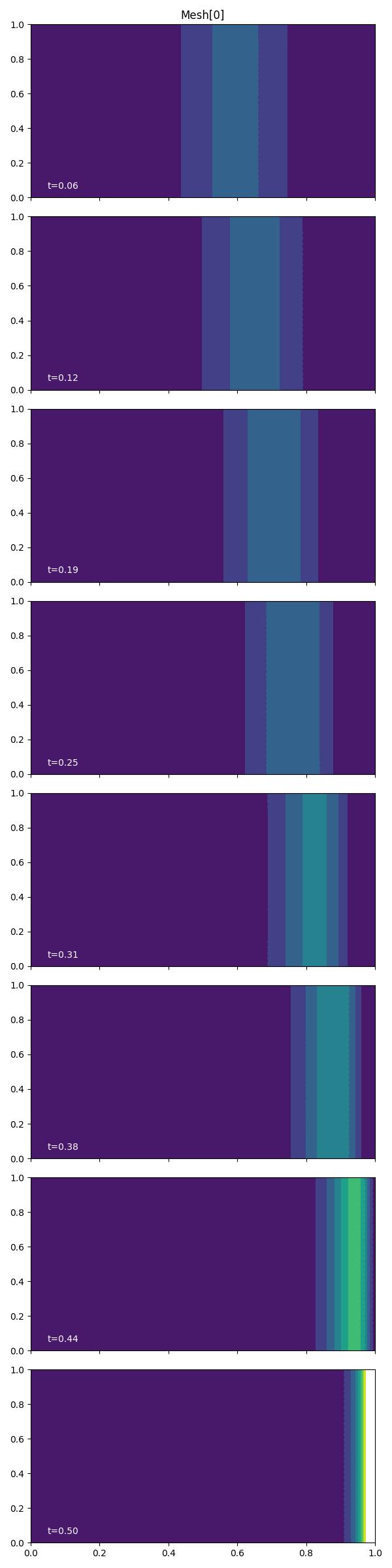
Since the arrow of time reverses for the adjoint problem, the plots should be read from bottom to top. The QoI acts as an impulse at the final time, which propagates in the opposite direction than information flows in the forward problem.
In the next demo, we solve the same problem on two subintervals and check that the results match.
This demo can also be accessed as a Python script.