Movement of a doubly periodic mesh driven by a Monge-Ampère type equation¶
In the previous demo, we demonstrated mesh movement with the Monge-Ampère method, driven by a ring shaped monitor function. In this demo, we solve the same problem but on a doubly periodic mesh.
Begin by importing from the namespaces of Firedrake and Movement.
from firedrake import *
from movement import *
Create a doubly periodic mesh with the same resolution as in the previous demo.
n = 20
mesh = PeriodicUnitSquareMesh(n, n)
Define the same monitor function and an instance of the
MongeAmpereMover class. ::
class.
def ring_monitor(mesh):
alpha = Constant(20.0)
beta = Constant(200.0)
gamma = Constant(0.15)
x, y = SpatialCoordinate(mesh)
r = (x - 0.5) ** 2 + (y - 0.5) ** 2
return Constant(1.0) + alpha / cosh(beta * (r - gamma)) ** 2
rtol = 1.0e-08
mover = MongeAmpereMover(mesh, ring_monitor, method="quasi_newton", rtol=rtol)
mover.move()
This should give command line output similar to the following:
0 Volume ratio 11.49 Variation (σ/μ) 9.71e-01 Residual 9.19e-01
1 Volume ratio 7.98 Variation (σ/μ) 6.71e-01 Residual 5.12e-01
2 Volume ratio 5.60 Variation (σ/μ) 5.40e-01 Residual 3.58e-01
3 Volume ratio 7.09 Variation (σ/μ) 4.89e-01 Residual 2.98e-01
4 Volume ratio 5.60 Variation (σ/μ) 4.54e-01 Residual 2.58e-01
5 Volume ratio 7.48 Variation (σ/μ) 4.31e-01 Residual 2.22e-01
6 Volume ratio 6.91 Variation (σ/μ) 4.16e-01 Residual 2.07e-01
7 Volume ratio 8.46 Variation (σ/μ) 4.03e-01 Residual 1.82e-01
8 Volume ratio 7.68 Variation (σ/μ) 3.93e-01 Residual 1.71e-01
9 Volume ratio 7.65 Variation (σ/μ) 3.94e-01 Residual 1.60e-01
10 Volume ratio 7.51 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
11 Volume ratio 7.49 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
12 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
13 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
14 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
15 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
16 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
17 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
18 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
19 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
20 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
21 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
22 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
23 Volume ratio 7.48 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
24 Volume ratio 7.47 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
25 Volume ratio 7.43 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
26 Volume ratio 7.43 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
27 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
28 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
29 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
30 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
31 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
32 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
33 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
34 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
35 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
36 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
37 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
38 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
39 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
40 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
41 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
42 Volume ratio 7.42 Variation (σ/μ) 3.93e-01 Residual 1.59e-01
43 Volume ratio 7.58 Variation (σ/μ) 3.95e-01 Residual 1.60e-01
44 Volume ratio 7.80 Variation (σ/μ) 3.97e-01 Residual 1.60e-01
45 Volume ratio 8.32 Variation (σ/μ) 4.09e-01 Residual 1.70e-01
46 Volume ratio 9.19 Variation (σ/μ) 4.22e-01 Residual 1.84e-01
47 Volume ratio 9.70 Variation (σ/μ) 4.29e-01 Residual 1.78e-01
48 Volume ratio 9.40 Variation (σ/μ) 4.01e-01 Residual 1.29e-01
49 Volume ratio 10.47 Variation (σ/μ) 4.03e-01 Residual 1.04e-01
50 Volume ratio 9.84 Variation (σ/μ) 3.72e-01 Residual 8.48e-02
51 Volume ratio 10.24 Variation (σ/μ) 3.87e-01 Residual 7.56e-02
52 Volume ratio 9.07 Variation (σ/μ) 3.61e-01 Residual 5.80e-02
53 Volume ratio 9.81 Variation (σ/μ) 3.73e-01 Residual 4.61e-02
54 Volume ratio 8.79 Variation (σ/μ) 3.56e-01 Residual 3.42e-02
55 Volume ratio 9.36 Variation (σ/μ) 3.63e-01 Residual 2.55e-02
56 Volume ratio 8.79 Variation (σ/μ) 3.52e-01 Residual 1.92e-02
57 Volume ratio 9.10 Variation (σ/μ) 3.57e-01 Residual 1.44e-02
58 Volume ratio 8.79 Variation (σ/μ) 3.51e-01 Residual 1.11e-02
59 Volume ratio 8.96 Variation (σ/μ) 3.53e-01 Residual 8.45e-03
60 Volume ratio 8.79 Variation (σ/μ) 3.50e-01 Residual 6.54e-03
61 Volume ratio 8.89 Variation (σ/μ) 3.51e-01 Residual 5.04e-03
62 Volume ratio 8.79 Variation (σ/μ) 3.49e-01 Residual 3.88e-03
63 Volume ratio 8.85 Variation (σ/μ) 3.50e-01 Residual 2.99e-03
64 Volume ratio 8.80 Variation (σ/μ) 3.49e-01 Residual 2.27e-03
65 Volume ratio 8.83 Variation (σ/μ) 3.49e-01 Residual 1.73e-03
66 Volume ratio 8.80 Variation (σ/μ) 3.49e-01 Residual 1.29e-03
67 Volume ratio 8.82 Variation (σ/μ) 3.49e-01 Residual 9.63e-04
68 Volume ratio 8.80 Variation (σ/μ) 3.49e-01 Residual 6.87e-04
69 Volume ratio 8.82 Variation (σ/μ) 3.49e-01 Residual 4.97e-04
70 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 3.34e-04
71 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 2.29e-04
72 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 1.41e-04
73 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 8.91e-05
74 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 4.84e-05
75 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 2.72e-05
76 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 1.43e-05
77 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 1.07e-05
78 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 7.66e-06
79 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 5.59e-06
80 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 3.89e-06
81 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 2.76e-06
82 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 1.86e-06
83 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 1.28e-06
84 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 8.23e-07
85 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 5.42e-07
86 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 3.29e-07
87 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 2.04e-07
88 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 1.13e-07
89 Volume ratio 8.81 Variation (σ/μ) 3.49e-01 Residual 6.46e-08
Solver converged in 89 iterations.
Again, plot the adapted mesh:
import matplotlib.pyplot as plt
from firedrake.pyplot import triplot
fig, axes = plt.subplots()
triplot(mover.mesh, axes=axes)
axes.set_aspect(1)
plt.savefig("monge_ampere_periodic-adapted_mesh.jpg")
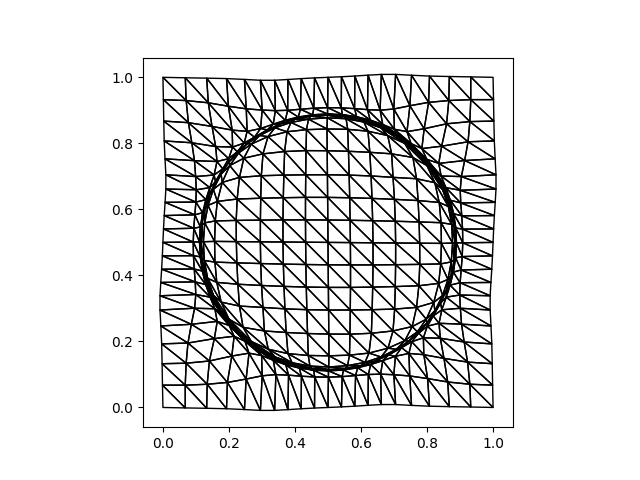
Observe that the outer boundary of the mesh is no longer square - each boundary segment has been warped. However, you might be able to convice yourself that the warp of the left boundary matches that of the right and that the warp of the top boundary matches that of the bottom. To be absolutely certain, let’s check that the area of the mesh matches expectations. We can do this by simply integrating unity over the domain associated with the adapted mesh.
import numpy as np
expected_area = 1.0
assert np.isclose(assemble(Constant(1.0) * dx(domain=mover.mesh)), expected_area)
Exercise
Looking at the solver output above, you might notice that the residual progress stalls for quite a few iterations before descending. Why might this be? Set up this demo and the previous one to record the residual values during the iteration. Re-run them and create a plot to compare the convergence progress on the same axes.
In the next demo, we will demonstrate that the Monge-Ampère method can also be applied in three dimensions.
This tutorial can be dowloaded as a Python script.
References